1           Dijkstra算法介绍

在数学上，以某个节点为起点，计算到其他节点的最短路径的算法，称为“单源最短路径” 算法。求“单源最短路径”的问题在数学上可以精确描述如下：

“单源最短路径” 问题：已知一个由n个节点(V0..n)构成的有向连通图G＝（V，E），以及图中边的权函数C (E)，其中V代表节点集合，E表示所有边的集合，并假设所有权非负，求由G中指定节点V0到其他各个节点的最短路径。

Dijkstra算法是很经典的求解上述问题的算法，其基本想法是设计一种最短路径树的构造方法，按非降次序逐条构造从V0到各个节点的最短路径，第一步找到和V0相距最短的节点以及到这个节点的路径，第二步找到和V0相距次短的节点以及到这个节点的路径，如此反复，最后找到V0到所有节点的最短路径，构造出整棵最短路径树。

对上述构造方法，直觉上很容易有如下思考：和V0相距最短的节点应该在和V0直接相邻的节点中，和V0相距次短的节点要么在和V0直接相邻的节点中，要么在和这些相邻节点相邻的节点中，如此逐步扩散考虑，应该就可以找到和V0相距最短、次短、…….第n短的节点以及对应的路径，而且因为是连通图，最后肯定所有节点都能全部考虑到，也就能完成整棵最短路径树的构造。

事实上，上述直觉非常有效，Dijkstra算法是对上述过程的一个提炼和优化：和V0相距最短的节点是和V0直接相连的节点没错；相距次短的节点范围可以缩小为，和V0直接相邻的节点，加上跟刚选中的最短节点直接相邻的节点；相距第三短的节点的范围可以类推得到，即在上一步考察的节点的基础上，加上和次短节点直接相邻的节点。如此逐步构造，可以按非降次序给出到所有节点的最短路径。

为了从数学上精确描述上述构造过程，需要引入了集合的概念对节点和路径进行分类。

我们把节点分成两个集合：

A：已经选入最短路径树的节点的集合。

B：剩余的其他节点的集合。

对于路径，我们分成三个集合：

I：已经选入最短路径树的路径的集合

II：候选路径集合：下一条加入最短路径树的路径将从这个集合中选入。

III：剩余的其他路径的集合（被废弃的路径或者还未考虑的路径）。

为了更好的理解，有必要对“路径”的定义进行明确和强调：路径是指以V0为起点，其他节点为终点的由一条或多条边组成的一个有序集。边，可以理解为路径中的一段，只有到和V0直接相邻的节点的路径才直接对应一条边。从V0到所有节点，都可能存在一条或多条路径，非最短路径在计算过程中将会被废弃，放入集合III。

从前面的描述中可以明显看出，Dijkstra算法是一个递归构造过程，因为任何递归都必须有明确的初始状态，所以我们有必要先得到上述Dijkstra算法中定义的集合的初始值：

l         以V0为起点计算最短路径的话，初始状态时显然有且只有V0在集合A中，所以集合A的初始值为V0。集合B的初始值为剩余节点。

l         前面提到过，下一个加入集合A的节点，一定是和V0直接有边相连的节点，因此，加入最短路径树的第一条路径也必然在这些和V0直接相连的边所代表的路径中产生，所以集合II的初始值就是和V0直接相连的边构成的路径。另外，初始状态最短路径树为空，所以集合I的初始值为空。集合I、II明确了的话，集合III自然明确。

 

下面我们开始展开递归构造最短路径树的过程：

l         第一步：从集合II中选择一条最短的路径，放入最短路径树，相应的，这条路径的终点对应的节点（这里记为X）应该从集合B移入集合A。

l         第二步：考察所有从X出发的边的终点，考虑其中不属于集合A的节点，这里记为Y，计算从V0出发经X到达Y的路径值，计算方法为：最短路径树中V0到节点X的路径值加上（X，Y）这条边的值。为了描述方便，我们把从V0出发经X到达Y的路径记为（V0X）Y。接着考察集合II中的候选路径，如果其中没有到节点Y的路径，则直接把路径(V0X)Y作为候选路径加入集合II；如果集合II中已经有到节点Y的路径，则进行比较，如果这条路径值小于或等于路径 (V0X)Y的路径值，那么路径 (V0X)Y作为被废弃的路径放入集合III，否则原集合II中到Y的路径被废弃放入集合II，（V0X）Y作为候选路径放入集合II。对于Y节点有多个的情况，按第二步的方法一个一个的计算和比较。

l         重复第一步和第二步，直到集合II和集合B为空。

第二步事实上是对候选路径的一个重新计算过程，因为在集合A中引入了新的节点后，考察的范围变大了，很可能在原来节点范围内认为到某个节点的最短路径已经不再是最短路径了，这时候，需要根据第二步的方法进行调整。

为了让大家更好的理解这一构造过程，这里举一个较为典型的例子，如下是一个有向图：

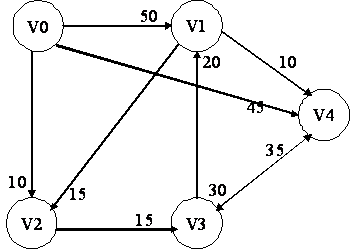
计算这个有向连通图的最短路径树的过程如下：

 

候选路径集合	路径长度	最短路径树中的节点(集合A)	最短路径树	说明
V0V1 V0V2 V0V4	50 10 45	V0	Null	在初始状态，最短路径树中只有节点V0，候选路径就是V0直接相连的边代表的路径。
V0V1 V0V4 V0V2V3	50 45 35	V0、V2	V0V0 V0V2	V0V2在所有候选路径中最短，所以放入最短路径树，V2放入集合A。考察所有以刚放入集合A的节点V2为起点的边的终点，对其中不在集合A中的节点，这里只有节点V3，计算从V0出发经节点V2，到达V3的路径V0V2V3的值，因为候选路径中没有到V3的路径，所以V0V2V3路径直接放入候选路径集合。
V0V4 V0V2V3V1	50 45 45 55	V0、V2、V3	V0V0 V0V2 V0V2V3	V0V2V3在所有候选路径中最短，所以放入最短路径树，V3放入集合A。考察所有以刚放入集合A的节点V3为起点的边的终点，对其中不在集合A中的节点，这里是节点V1，V4，计算从V0出发经节点V3，到达这两个节点的路径V0V2V3V1和V0V2V3V4的路径值，并和候选路径中已有的到达V1、V4的路径值进行比较：V0V2V3V1小于V0V1，所以V0V1从候选路径中删除，V0V2V3V1放入候选路径集合；V0V2V3V4比V0V4大，所以V0V4在候选路径中保留，V0V2V3V4路径废弃不用。
V0V2V3V1	45	V0、V2、V3、V4	V0V0 V0V2 V0V2V3 V0V4	V0V4和V0V2V3V1路径值相等，任意选择V0V4放入最短路径树，V4放入集合A。考察所有以刚放入集合A的节点V4为起点的边的终点，其中不在集合A中的节点没有（虽然有边V4V3，但V3已经在集合A中了），所以不进行选择和计算。
		V0、V2、V3、V4、V1	V0V0 V0V2 V0V2V3 V0V4 V0V2V3V1	候选路径V0V2V3V1放入最短路径树，这时候选路径集合为空，并且所有节点已经放入了集合A。计算结束。

 

2           Dijkstra算法的证明

对Dijkstra算法进行证明，实际上就是要证明其构造过程构造的树一定是最短路径树。为了给出证明，我们先分析一下构造过程。

分析构造过程的第二步，可以得出结论一。

结论一：对一个还没有选入集合A的节点Y，其候选路径是所有从V0出发，中途只经过集合A中的节点到达Y的路径中路径值最小的。

这个结论根据第二步候选路径的构造过程，很容易得出：因为在第一次构造到Y的候选路径时，从V0出发经刚加入集合A的节点到Y的路径，是被直接放入候选路径集合中的，这说明第一次构造的到Y的候选路径满足条件“从V0出发，中途只经过集合A中的节点”。另外，集合A中每加入一个新节点，都会考虑从V0出发经过这个新节点到达Y的路径，并和原候选路径比较，选择两者中较小的那个，这种过程一直持续到Y被选入集合A中为止。这个过程显然保证了Y的候选路径一直保持了特性“从V0出发，中途只经过集合A中的节点”，而且因为遍历了所有A中的节点，所以是所有这种特性路径中最短的。

 

有了结论一，证明Dijkstra算法可以弱化为证明结论二。

结论二：假设构造过程中下一步将选择的是节点Y，那么这时到达Y的最短路径必然是从V0出发，中途只经过集合A中的节点到达Y的路径。

如果“结论二”成立的话，结合“结论一”，说明Y的最短路径和候选路径具有相同的属性“从V0出发，只经过集合A中的节点”，而“结论一”中明确说明，候选路径是这种属性的路径中的最小者，所以对于下一步即将选入集合A中的节点Y，其最短路径值就是候选路径，也即证明了算法中构造最短路径树过程的正确性。

下面我们证明“结论二”。

证明很简单，使用反证法：假设到达Y的最短路径中途不只经过集合A，那么必然经过一个不在集合A中的节点W，于是这条路径中肯定包含一条从V0到W的路径，这条路径显然比从V0出发经过W到Y的路径更短，而Y是下一步要放入集合A中的节点，根据我们按非降次序构造最短路径树的过程（第一条最短，第二条次短…..），从V0出发到W的这条路径应该已经在最短路径树中了，也即节点W应该已经在集合A中，矛盾，得证。

3           OSPF协议中对Dijkstra算法的使用

从理论上来说，只要描述清楚了节点之间的连接和边的属性，就描述清楚了有向图，也就可以使用Dijkstra算法计算出最短路径树。

对于使用基于Dijkstra算法的路由协议来说，如果能描述清楚整个网络拓扑（对应有向图），并让区域内的每台路由器都清楚的知道整个区域的网络拓扑，则每台路由器就可以独立的计算出最短路径树。从这个意义上说，对于一个使用Dijkstra算法的路由协议来说，需要解决以下问题：

l         网络拓扑的描述；

l         网络拓扑描述信息的传播；

l         效率：在耗费最少资源（带宽、内存、CPU）的情况下，最短时间内动态计算到其他网段的最优路径。

其他需要考虑的问题还包括，路由协议的定位（IGP还是EGP？用于多大网络？），路由协议的鲁棒性，与其他路由协议某种程度的互操作等。

以上几个问题有一定的相关性，互相影响。例如，网络拓扑描述的优化可以减少描述信息，从而减轻传播和计算过程的消耗，提高效率。

本文的着力点是Dijkstra算法及其在OSPF中的应用，所以这里只说明与之相关的网络拓扑的描述和最短路径计算两个内容，网络拓扑的描述也只涉及的几类基本LSA。

3.1         OSPF对网络拓扑的描述

OSPF中使用链路状态通告（LSA）来描述网络拓扑（即有向图）。

OSPF中，Router LSA被用来描述路由器（节点）之间的连接和链路（边）的属性，具备了理论上计算最短路径的可能。但是仅仅是理论而已，从实践的角度，针对特殊的网络情况和应用场景，需要作一些优化工作。

先考虑一个有n个节点的广播网，如果使用Router LSA来描述的话，需要描述n个节点两两相连的n*(n-1)/2条链路，而且n个节点间需要建立建立n*(n-1)/2个邻接关系，描述信息需要在这些建立了邻接关系的节点间传播，会消耗大量资源。如果换一种思路，我们把这个广播网虚构成一个伪节点，其他n个节点均和伪节点相连，那么就只要描述n条链路，n个节点只需要和伪节点建立总共n个邻接关系即可，能大大减少信息描述量和信息传播量。根据这个思路，OSPF中针对广播网的描述进行了优化，使用指定路由器DR来承担这个伪节点的角色，并使用Network  LSA来描述广播网内DR和各个路由器的连接情况。

对于NBMA网络的描述，处理方式和广播网基本相同。

其次，OSPF的设计目标是为一个较大的内部网络提供动态路由能力。如果内部网络较大的话，需要描述的链路会很多，存储、传播和计算这些链路信息将耗费大量带宽、内存和CPU资源。OSPF解决这个问题的办法是把较大的网络划分成多个Area，每个Area内部使用Router LSA和Network LSA把Area内部网络拓扑描述清楚，并据此使用Dijkstra算法计算出本Area内的最短路径树和路由。至于Area外的网络拓扑，区域边界路由器ABR并不把相邻Area的Router LSA和Network LSA传入本Area，而是把自己在相邻Area范围内计算得到的各个网段的路由进行汇总，把这些网段当做直接连接在自己上面，并生成Network Summary LSA来对这些网段进行描述，传入本Area。这样，对于一个有n个网段和多台路由器的相邻Area，ABR只需要生成n条网络描述信息并传入本Area即可，大大减少了进入本Area的链路描述信息，减少了存储、传播和计算消耗。需要注意的是，划分Area的做法导致了Area内部路由器中的链路状态数据库描述的Area外部分并不是真实的网络拓扑，从而计算时可能出现环路，为了避免环路出现，要求所有的Area之间的相连必须经过Backbone区域即Area 0。

另外，OSPF被设计为一个IGP，除了处理本自治系统内的路由外，还需要处理自治系统外的路由，这类路由在ASBR处引入，可以看做是直接连接在ASBR上，OSPF引入AS External LSA来描述这类自治系统外路由。另外，因为AS External LSA在传入其他Area时并不在ABR上重新生成，所以从计算的角度看，其他Area还必须知道自治系统外路由从哪个节点引入，所以需要引入ASBR Summary LSA来描述外部路由从哪个节点引入，ASBR Summary LSA在ABR上生成，从其他Area看，可以认为于ASBR直接连在ABR上，自治系统外部路由对应的网段又直接连在ASBR上。

3.2         OSPF中最短路径的计算

下面简单介绍一下OSPF的最短路径计算过程，具体的细节处理请参考RFC2328：

首先，计算Area内部路由。因为Router LSA和Network LSA精确的描述出了整个Area内部的网络拓扑，所以根据Dijkstra算法，可以计算出到各个节点（路由器）的最短路径。然后根据Router LSA描述的与路由器相连的网段情况，就得到了到各个网段的最短路径。注意，计算过程中，如果有多条代价相同的最短路径，都保留。

其次，计算跨Area的路由。因为从一个Area内部看，相邻Area的路由对应的网段就好像是直接连在ABR上，而到ABR的最短路径已经在上一步算出，所以直接检查Nerwork Summary LSA，就可以很容易得到这些网段的最短路径值。另外，ASBR也被看做是直接连接在ABR上，所以到ASBR的最短路径也可在这一步计算出来。注意：在这一步，如果发起计算的路由器是ABR，那么很自然，应该只考虑骨干区域的Network Summary LSA；但是对于启用了Virtual Link的拓扑来说，跨Area的路由只是逻辑上通过骨干区域，而实际是通过Transit Area到达的，因为逻辑链路可能并不是物理上最优的，所以在连接到Transit Area的ABR上，考察骨干区域的Network Summary LSA得到的跨Area路由的路径可能不最优，还需要考察Transit Area的Network Summary LSA，以得到最短路径。

最后，计算AS外部路由，因为AS外部路由可以看做是直接连接在ASBR上，而到ASBR的最短路径在上一步已经计算出来，所以逐条检查AS External LSA就可以得到到各个外部网络的最短路径。

3.3         下一跳和出接口

路由表中还有两个重要元素：下一跳和出接口。因为确定这两个元素和计算过程有一定关系，这里也提一下。

其实，一个简单事实是，对于任何一条路径来说，其下一跳和出接口，必然和他的父路径的下一跳和出接口相同。因此，确定所有路径的下一跳和出接口，最后可以归结为确定到“和V0直接相连的节点”的下一跳和出接口。对于OSPF来说，“和V0直接相连的节点”要么是一台路由器，要么是一个伪节点（广播网、NBMA网络中使用了DR模拟伪节点）。

前面Dijkstra算法已经提到，确定到各个节点或网段的最短路径的过程，是一个候选路径的构造和调整过程，在这个过程中，候选路径的父路径会进行多次调整，但其根都跳不出和“V0直接相连的节点”这一范围，因此其下一跳和出接口也在“和V0直接相连的节点”的下一跳和出接口的范围内，在计算过程中继承即可。

确定“和V0直接相连的节点”的下一跳和出接口比较简单，这里不再赘述，想了解的话可以参考RFC2328的16.1.1节。

还有一类特殊的网段是发起OSPF计算的节点的直连网段，其下一跳和出接口的确定就更直接了，而且不会被其他路径继承。